library(tidyverse)
set.seed(57291)

Functional programming is another programming paradigm like object oriented programming.

It’s style that works quite well in R, because R has first class functions – you can do anything with a function that you can do with a regular value.

We’ll touch on three techniques:

All using functions in the purrr package

Resources: https://adv-r.hadley.nz/fp.html

Functionals

You are already familiar with the map()!

map(.x, .f, ...)

.f a function to apply to each element

The rest of the family…

reduce()

reduce(.x, .f)

.f is some function that takes two values and returns a single value.

reduce() iteratively applies .f to .x to reduce many values to one.

E.g. reduce(.x = c(1, 2, 3, 4), .f = f) is equivalent to:

f(f(f(1, 2), 3), 4) # OR equally
1 %>% f(2) %>% f(3) %>% f(4)

Your turn Guess what the output will be, then run to check Hint: `+`(1, 2) is the same as 1 + 2

reduce(c(1, 2, 3, 4), `+`)

The same as

(((1 + 2) + 3) + 4)
## [1] 10
sum(1:4)
## [1] 10

A more interesting example

baskets <- list(
  c("bread", "milk", "apples", "bananas"),
  c("milk", "cheese", "bread"),
  c("ham", "salami", "milk"),
  c("milk", "ham", "apples", "bananas")
)

Which items are in every basket?

One approach is to think about the set intersection of all the baskets.

intersect(baskets[[1]], baskets[[2]])
## [1] "bread" "milk"
reduce(baskets, intersect)
## [1] "milk"

What is the complete list of possible items in the baskets?

reduce(baskets, union)
## [1] "bread"   "milk"    "apples"  "bananas" "cheese"  "ham"     "salami"
# A non- reduce() solution
unlist(baskets) %>% unique()
## [1] "bread"   "milk"    "apples"  "bananas" "cheese"  "ham"     "salami"

map-reduce

Idea behind map-reduce a framework for working with large data sets – in the map step, workers do the map operation on the data they have, then a single process reduces all the results into one.

Functional operators

Motivation

Imagine simulating 100 AR(1) time series with parameter \(\alpha = 0.95\):

ar1_series <- rerun(100, 
  arima.sim(model = list(ar = 0.95), n = 20))

You can fit the model to one series with arima() (does a numerical optimization to get MLE, started from conditional least squares estimates):

arima(ar1_series[[1]], order = c(1, 0, 0))
## 
## Call:
## arima(x = ar1_series[[1]], order = c(1, 0, 0))
## 
## Coefficients:
##          ar1  intercept
##       0.6099    -0.7289
## s.e.  0.1971     0.5903
## 
## sigma^2 estimated as 1.194:  log likelihood = -30.38,  aic = 66.77

We might be interested in investigating the performance of an estimate for \(\alpha\):

map(ar1_series, arima, order = c(1, 0, 0))
## Error in .f(.x[[i]], ...): non-stationary AR part from CSS

On which iteration did the error arise? How can we keep going without one error stopping all our iteration?

safely() a functional operator

safe_log <- safely(log)

Your turn What kind of object is safe_log?

Compare the output of the following:

log(10)
safe_log(10)
log("a")
## Error in log("a"): non-numeric argument to mathematical function
safe_log("a")

safely()returns a function that always returns a list with two elements result and error, one of which is always NULL

Putting it to good use

safely(arima)
## function (...) 
## capture_error(.f(...), otherwise, quiet)
## <bytecode: 0x7fa505ec1a00>
## <environment: 0x7fa508051348>

Now this runs without stopping:

ar1_fits <- map(ar1_series, safely(arima), order = c(1, 0, 0))
## Warning in .f(...): possible convergence problem: optim gave code = 1

But the output is a little awkward:

ar1_fits[1:2]
## [[1]]
## [[1]]$result
## 
## Call:
## .f(x = ..1, order = ..2)
## 
## Coefficients:
##          ar1  intercept
##       0.6099    -0.7289
## s.e.  0.1971     0.5903
## 
## sigma^2 estimated as 1.194:  log likelihood = -30.38,  aic = 66.77
## 
## [[1]]$error
## NULL
## 
## 
## [[2]]
## [[2]]$result
## 
## Call:
## .f(x = ..1, order = ..2)
## 
## Coefficients:
##          ar1  intercept
##       0.6817     3.2588
## s.e.  0.1750     0.5204
## 
## sigma^2 estimated as 0.5985:  log likelihood = -23.56,  aic = 53.12
## 
## [[2]]$error
## NULL
ar1_fits[1:5] %>% str(max.level = 2)
## List of 5
##  $ :List of 2
##   ..$ result:List of 14
##   .. ..- attr(*, "class")= chr "Arima"
##   ..$ error : NULL
##  $ :List of 2
##   ..$ result:List of 14
##   .. ..- attr(*, "class")= chr "Arima"
##   ..$ error : NULL
##  $ :List of 2
##   ..$ result:List of 14
##   .. ..- attr(*, "class")= chr "Arima"
##   ..$ error : NULL
##  $ :List of 2
##   ..$ result:List of 14
##   .. ..- attr(*, "class")= chr "Arima"
##   ..$ error : NULL
##  $ :List of 2
##   ..$ result:List of 14
##   .. ..- attr(*, "class")= chr "Arima"
##   ..$ error : NULL

We need to find the elements where the error element isn’t NULL.

transpose() turns a list inside out:

ar1_fits_t <- transpose(ar1_fits)
ar1_fits_t %>% str(max.level = 1)
## List of 2
##  $ result:List of 100
##  $ error :List of 100

Which makes it easy to find the elements without an error:

ok <- map_lgl(ar1_fits_t$error, is.null)

And use that to pull out the errors, or which samples produced them:

ar1_fits_t$error[!ok] # what were the errors
## [[1]]
## <simpleError in .f(...): non-stationary AR part from CSS>
## 
## [[2]]
## <simpleError in .f(...): non-stationary AR part from CSS>
## 
## [[3]]
## <simpleError in .f(...): non-stationary AR part from CSS>
ar1_series[!ok]  # which series generated them
## [[1]]
## Time Series:
## Start = 1 
## End = 20 
## Frequency = 1 
##  [1] -3.3534368 -3.0951481 -3.0516036 -4.7160478 -4.7480772 -5.7081727
##  [7] -5.2347177 -5.2526778 -5.0563317 -4.0665666 -4.9653963 -5.7939490
## [13] -5.8242676 -3.0556686 -1.7263417 -0.5358495  1.7128079  2.2412037
## [19]  4.1916670  4.4768658
## 
## [[2]]
## Time Series:
## Start = 1 
## End = 20 
## Frequency = 1 
##  [1] -0.36068860  0.24861314 -0.41445358 -1.14363445 -0.93666186
##  [6] -0.02801535  0.94656881  1.00018206  1.65730761  3.27611153
## [11]  2.98063259  3.06498382  3.40821958  2.14774649  1.63483418
## [16]  1.00621711 -0.78402215 -1.29709084 -3.14324946 -3.89710475
## 
## [[3]]
## Time Series:
## Start = 1 
## End = 20 
## Frequency = 1 
##  [1]  5.2788934  4.9829612  3.9225622  3.5281228  2.8421032  3.8841123
##  [7]  4.8598289  6.1408107  5.3025480  6.6070733  5.6165941  4.5296112
## [13]  2.9581368  1.2483577  0.7783952 -1.0070619 -1.7582732 -2.9540844
## [19] -3.3423897 -4.3291866

Your turn Use ok to pull out the elements that successfully fit, and find the estimate of \(\alpha\) from each one.

ar1_fits_t$result[ok] %>% 
  map(coef) %>% 
  map_dbl(1)

## OR
ar1_fits_t$result[ok] %>% 
  map("coef") %>% 
  map_dbl(1) %>% 
  hist()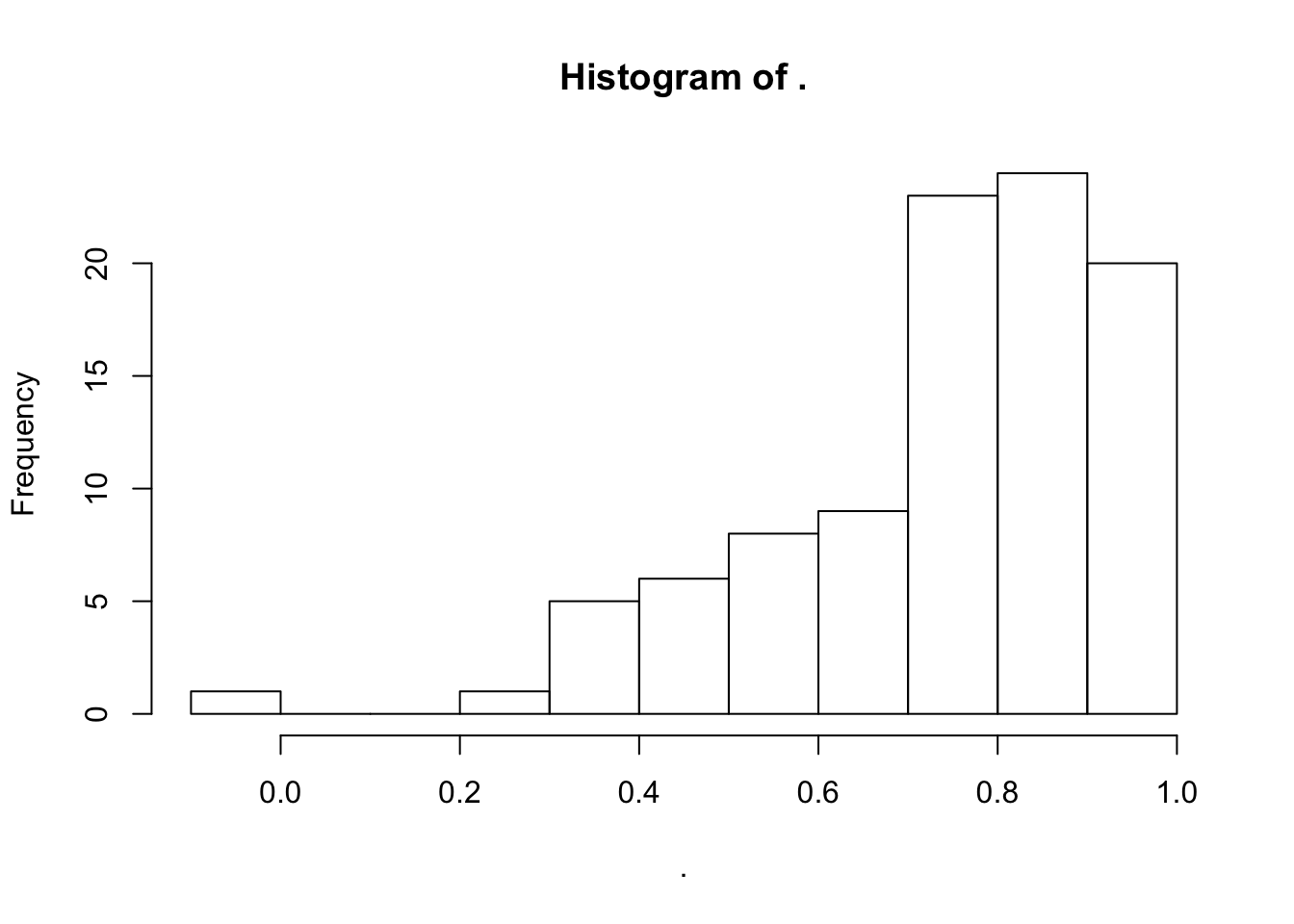

Also see possibly() and quietly()

possibly() doesn’t capture the error, it just returns a default value you specify:

estimate_alpha <- function(x){
  arima(x, order = c(1, 0, 0)) %>% coef() %>% pluck(1)
}
map_dbl(ar1_series, 
  possibly(estimate_alpha, otherwise = NA, quiet = FALSE))
## Error: non-stationary AR part from CSS
## Error: non-stationary AR part from CSS
## Error: non-stationary AR part from CSS
## Warning in arima(x, order = c(1, 0, 0)): possible convergence problem:
## optim gave code = 1
##   [1]  0.6099325  0.6816754  0.8255509  0.5404877  0.8281109  0.7325073
##   [7]  0.6672460         NA  0.6992435  0.8318520  0.7837984  0.8435008
##  [13]  0.6603792  0.9109857  0.9441183  0.3017143  0.9379027  0.7203600
##  [19]  0.9464088  0.8573701  0.7976971  0.8258578  0.9794134  0.8057567
##  [25]  0.8971668  0.3627412  0.7592842  0.8193397  0.9109259  0.8401488
##  [31]  0.7608817 -0.0761697  0.7934027  0.7605834  0.7116478  0.5251081
##  [37]  0.9234897  0.7893801  0.8782270  0.8483945  0.6645448  0.2908150
##  [43]  0.8809670  0.3087400  0.7294408         NA  0.8518711  0.4165418
##  [49]  0.9499480  0.4989194  0.9375076  0.7898615  0.3033989  0.3980182
##  [55]  0.8899871  0.9368759  0.7860537  0.9234076  0.9002606  0.8012560
##  [61]  0.8012382  0.4223826  0.5484254  0.9187579  0.7356023  0.5200131
##  [67]  0.6563350  0.5997682  0.8813759  0.5965004  0.7467530  0.4123580
##  [73]  0.8930968  0.5002282  0.7460675  0.8791760  0.7994180  0.9093477
##  [79]  0.4632585  0.8893103  0.7498224  0.6686794  0.7158937  0.6961227
##  [85]  0.7385590  0.9070601  0.9272516  0.9201210  0.5747246         NA
##  [91]  0.9599866  0.7453595  0.7692607  0.8863382  0.9829849  0.9671730
##  [97]  0.7060810  0.4204500  0.8737742  0.8585487

quietly() captures messages or warnings.

memoise::memoise()

Another useful functional operator is memoise::memoise(). It produces a version of the function that remembers which arguments is has been called with and can reuse already calculated outputs instead of recalculating them.

Function factories

Functions that create functions

E.g. from Advanced R

power1 <- function(exp) {
  force(exp)
  
  function(x) {
    x ^ exp
  }
}

square <- power1(2)
cube <- power1(3)
square(3)
## [1] 9
cube(3)
## [1] 27

Q: What’s does force() do? It forces the argument to be evaluated so you don’t end up with problems like this:

power2 <- function(exp) {
  function(x) {
    x ^ exp
  }
}

my_exp <- 2
my_square <- power2(my_exp)
my_exp <- 3
my_square(3)
## [1] 27

An application

From: https://adv-r.hadley.nz/function-factories.html#MLE

ML estimation of \(\lambda\) in a Poisson model.

If \(X_1, \ldots, X_n\) are i.i.d Poisson(\(\lambda\)), then the log likelihood is: \[ \ell(\lambda; x) = \log(\lambda)\sum_{i = 1}^n x_i - n\lambda - \sum_{i = 1}^{n}\log(x_i!) \]

x <- c(9L, 6L, 1L, 8L, 3L, 4L, 3L, 2L, 4L, 4L, 3L, 2L, 4L, 5L,
  3L, 3L, 5L, 8L, 4L, 8L)

Our previous approach

Write a function for the negative log-likelihood:

nllhood_poission1 <- function(lambda, x){
  -1 * (log(lambda)*sum(x) - length(x)*lambda - 
    sum(lfactorial(x)))
}

Optimize over lambda passing in x to optimize through ...:

optimize(nllhood_poission1, interval = c(0, 10), x = x) 
## $minimum
## [1] 4.450001
## 
## $objective
## [1] 43.13677

An alternative approach

Define a factory for poisson negative likelihoods:

nllhood_poission <- function(x){
  s_x <- sum(x)
  n <- length(x)
  s_fac_x <- sum(lfactorial(x))
  function(lambda){
    -1 * (log(lambda)*s_x - n*lambda - s_fac_x)
  }
}

Use it to create the function for our specific data:

nll1 <- nllhood_poission(x)
nll1
## function(lambda){
##     -1 * (log(lambda)*s_x - n*lambda - s_fac_x)
##   }
## <environment: 0x7fa5053d8ae0>
nll1(5)
## [1] 43.76526
optimize(nll1, interval = c(0, 10)) 
## $minimum
## [1] 4.450001
## 
## $objective
## [1] 43.13677

Advantages:

  • should be faster, since the computation of the data summaries only happens once (not on every call to nll1())

    bench::mark(
  nllhood_poission1(5, x = x),
  nll1(5)
)
    ## # A tibble: 2 x 10
##   expression       min     mean   median     max `itr/sec` mem_alloc  n_gc
##   <chr>       <bch:tm> <bch:tm> <bch:tm> <bch:t>     <dbl> <bch:byt> <dbl>
## 1 nllhood_po…   3.11µs   4.38µs   3.71µs 413.5µs   228278.      208B     1
## 2 nll1(5)        705ns 992.52ns    875ns  52.1µs  1007534.        0B     1
## # ... with 2 more variables: n_itr <int>, total_time <bch:tm>

  • code becomes closer to mathematical structure of the problem. E.g. given data we define a function of \(\lambda\), then maximize that function.