library(tidyverse)
library(here)
set.seed(183991)

Optimization

A bit of a change in topic. So far we’ve been using simulation to approximate the distribution of random variables.

Optimization doesn’t involve simulation, but it is an example of another area where a compuational approach is a useful alternative to an analytical one.

Group Activity

Imagine we have a function \(f(\cdot)\). We want to find \(x\) such that \(f(x)\) is as small as possible.

Run the code below to get a function f():

f <- read_rds(url("http://stat541.cwick.co.nz/notes/10-f.rds"))

In 10 minutes, the group with an x that gives the smallest value of f(x) wins.

Strategies

Some strategies people used:

  • Plot it, and look for minimum

  • Guess a number, try again.

  • Generate a large sequence, plotted function, zoomed in with new sequence and small sequence size. This is an example of a grid search - an official method of minimization, but it has a few downsides:

  • It might take a long time,
  • You might miss the minimum if it falls between your grid points.

  • The global minimum might be outside your grid.

ggplot(data.frame(x = c(-2, 2)), aes(x = x)) + 
  stat_function(fun = f)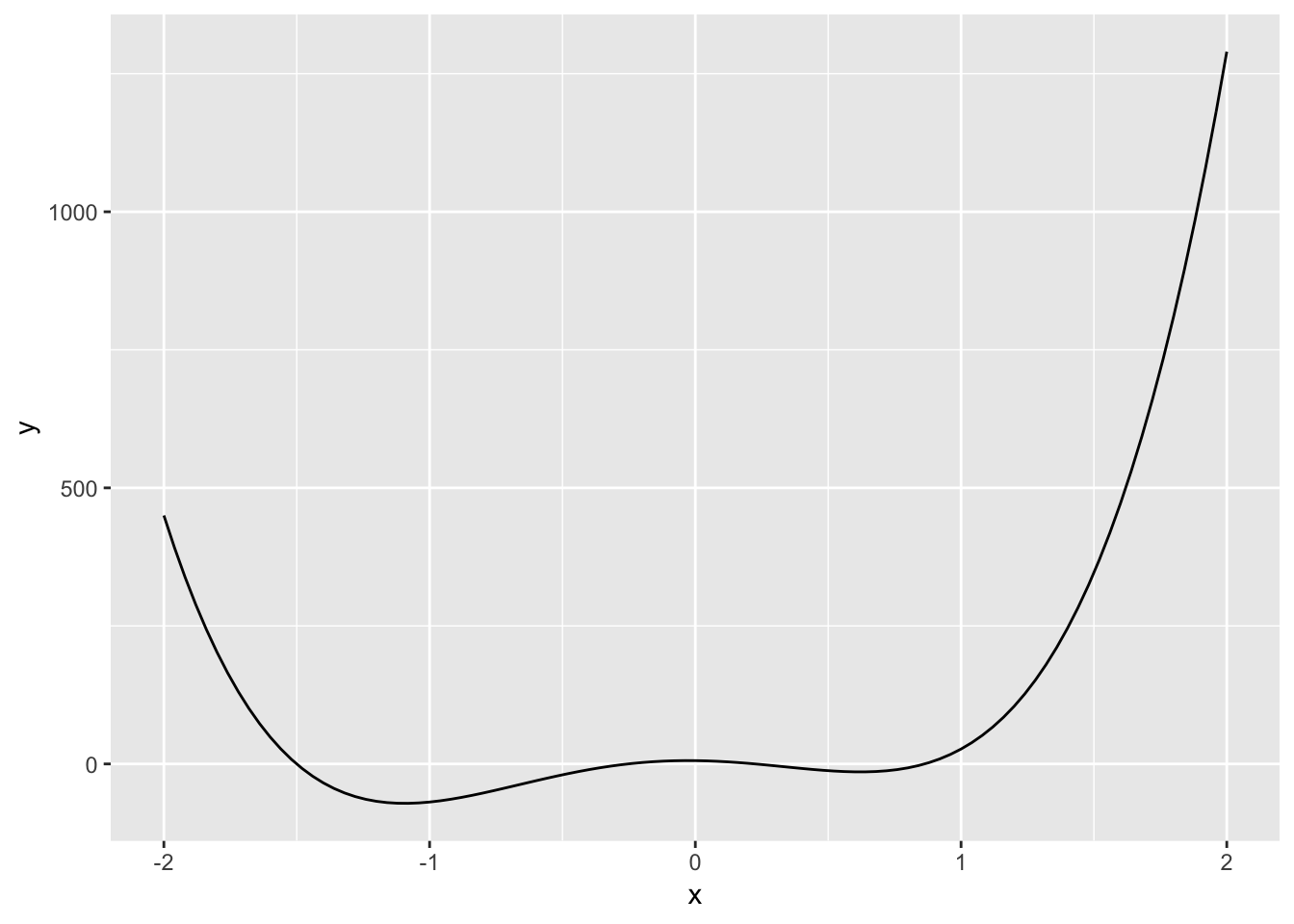

Objective of optimization

Given a function, \(f(.)\) find \(x\) such that \(f(x)\) is as large or small as possible.

How do we do it analytically?

  1. Take the derivative of \(f(x)\) w.r.t \(x\)
  2. Solve for \(f'(x) = 0\), to find critical points
  3. Check 2nd derivative at critical points, \(f''(x)>0\)

This gets you a local minima. (Might need to worry about boundary values for functions that are defined on some sub-interval of \(\mathbb{R}\))

E.g. Maximum Likelihood E.g. Linear Regression, fit by minimising squared residuals

It is enough to consider minimization, if we want to maximise \(f(\cdot)\), then minimise \(-f(\cdot)\).

A Maximum Likelihood Example

Let \(Y_1, \ldots, Y_n\) be i.i.d from some distribution with pdf \(f(\cdot; \theta)\) where \(\theta\) is an unknown parameter.

Then the maximum likelihood estimate of \(\theta\) is that value that maximises the likelihood given the data observed: \[ \hat{\theta} = \arg \max_{\theta} \mathcal{L}(\theta) \] where \(\mathcal{L}(\theta)\) is the likelihood function, and in this setting, is \[ \mathcal{L}(\theta) = \prod_{i= 1}^{n} f(y_i; \theta) \]

In practice it’s usually easier to usually work with the log liklihood: \[ l(\theta) = \log(\mathcal{L}(\theta)) = \sum_{i= 1}^{n} log(f(y_i; \theta)) \]

Bernoulli example

y <- c(0, 0, 1, 1, 0, 1, 0)

Let \(y_1, \ldots, y_n\) be i.i.d Bernoulli(\(\pi\)). What’s the maximum likelihood estimate of \(\pi\)?

\[ f(y_i, \pi) = \pi^{y_i} (1-\pi)^{(1-y_i)} \]

\[ l(\pi) = \sum_{i = 1}^{n} y_i \log(\pi) + (1- y_i)\log(1- \pi) \]

Maximise Analytically

Left as an exercise Find derivative, set to zero, solve for \(\pi\), find \(\hat{\pi} = \overline{y}\)

(pi_hat <- mean(y))
## [1] 0.4285714

Maximise Numerically

negative_llhood <- function(pi, y){
  -1* sum(y*log(pi) + (1-y)*log(1-pi))
}
optimize(f = negative_llhood, interval = c(0, 1), y = y)
## $minimum
## [1] 0.4285707
## 
## $objective
## [1] 4.780357

Simple logistic regression

Now imagine data come in pairs \((y_i, x_i), i = 1, \ldots, n\).

\(y_i \sim \text{ Bernoulli}(\pi_i)\), where

\[ \log{\frac{\pi_i}{1-\pi_i}} = \beta_0 + \beta_1 x_i \]

Implies \(\pi_i = \frac{\exp(\beta_0 + \beta_1 x_i)}{1 + \exp(\beta_0 + \beta_1 x_i)}\).

This is a simple logistic regression model.

\[ \mathcal{L(\beta_0, \beta_1)} = \prod_{i = 1}^{n} \pi_i^{y_i} (1-\pi_i)^{(1-y_i)} \] \[ \mathcal{l(\beta_0, \beta_1)} = \sum_{i = 1}^n y_i \log(\pi_i) + (1- y_i)\log(1- \pi_i) \]

To find \(\hat{\beta_0}\), \(\hat{\beta_1}\) need to solve: \[ \frac{\partial l}{\partial \beta_0} = 0 \\ \frac{\partial l}{\partial \beta_1} = 0 \\ \]

Can’t solve analytically, do numerically. Need method for bivariate functions.